Question

Dina is shipping a wall map to a collector. When the map is rolled up, it measures 7 ft long. She will use a box that is a right rectangular prism with a base that is 3 ft by 3 ft. Which whole number could be the shortest height of the box that will hold the map? Justify your answer.

A. 4 ft
B. 5 ft
C. 6 ft
D. 7 ft

Answer 1

6 ft

Explanation:

In the right triangle ABC connect points A and B

BC=3ft

AC=3ft

AB² =BC² + AC²=9+9=18ft²

In the right triangle ABD, AB²=18ft

BD=7ft

AB²+AD²=BD²

18+AD²=7²

AD²= 49-18

AD=
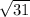`\sqrt{31\\` =5.6

the length of AD is a whole number, round it

AD=6ft {the shortest height}

Answer 2

Check the picture below.

`\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ c^2=a^2+o^2\implies c=√(a^2 + o^2) \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{b}\\ a=\stackrel{adjacent}{3}\\ o=\stackrel{opposite}{3} \end{cases} \\\\\\ b=√( 3^2 + 3^2)\implies b=√( 9 + 9 ) \implies b=√( 18 ) \\\\[-0.35em] ~\dotfill`

`\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=√(c^2 - a^2) \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{7}\\ a=\stackrel{adjacent}{√(18)}\\ o=\stackrel{opposite}{h} \end{cases} \\\\\\ h=\sqrt{ 7^2 - (√(18))^2}\implies h=√( 49 - 18 ) \implies h=√( 31 )\implies h\approx 6`