Question

In the Diagram to the right GKNM ~ VRPT

Find the value of X. Give the scale factor of the left polygon to the right polygon

X=
The scale factor of GKNM to VRPT is _:_

Answer 1

• x = 3.6

• The scale factor of GKNM to VRPT is 4 : 3.

Explanation:

If polygon GKNM is similar to polygon VRPT, then the corresponding sides are in the same ratio. Therefore:

`GK : VR = KN : RP = NM : PT = GM : VT`

Substitute the values and expressions of each side into the ratio:

`8.4 : 6.3 = (3x - 2) : (x + 3) = 4 : 3 = 4 : 3`

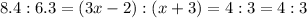
To find the value of x, we can use KN : RP = NM : PT.

`\begin{aligned}KN : RP &= NM : PT\\\\(3x - 2) : (x + 3) &= 4 : 3\\\\(3x - 2)/(x + 3) &= (4)/(3)\end{aligned}`

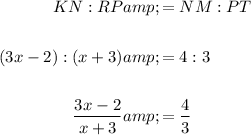
Cross-multiply and solve for x:

`\begin{aligned}(3x - 2)/(x + 3) &= (4)/(3)\\\\3(3x-2)&=4(x+3)\\\\9x-6&=4x+12\\\\5x&=18\\\\x&=3.6\end{aligned}`

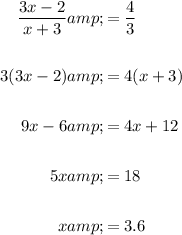
Therefore, the value of x is x = 3.6.

The scale factor of GKNM to VRPT is the ratio of the corresponding sides.

`\textsf{Scale factor}= NM : PT = 4 : 3`

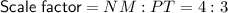
Therefore, the scale factor of GKNM to VRPT is 4 : 3.