Question

.HELPPPPPPPPPPPPPPPPP​

Answer 1

`\textsf{Choice A } \quad y = (5)/(3)x + 1`

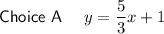
Explanation:

Slope intercept form of a line equation is

y = mx + b

where

m = slope

b = y-intercept

A perpendicular line to y = mx + b will have a slope of -1/m

Let's first find the equation for line z in slope-intercept form
Slope m for a line = (y2- y1)/(x2 - x1) where x1, y1 and x2, y2 are two points on the line

Slope of line z is

`m = \frac { 2 - (-1) }{-2 - 3} = (3)/(-5) = - (3)/(5)`

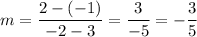
So line z will have an equation of the form

`y = -(3)/(5)x + b`

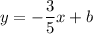
We know that a line perpendicular to this line will have a slope of

`- (1)/(-(3)/(5)) = (5)/(3)`

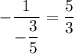
So the equation of the perpendicular line is

`y = (5)/(3)x + b`

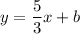
Only one of the 4 choices, name choice A has this slope of 5/3

Therefore the correct answer choice is A

There is no need to compute b, the y intercept but if you wanted to, this is how you would do it:

The perpendicular line passes through (3, 6). This means when x = 3, y =6

Substitute these values of x, y into the equation for the perpendicular line and solve for b

`y = (5)/(3)x + b\\\\\text{When x = 3, y = 6}:\\\\6 = (5)/(3) \cdot 3 + b\\\\6 = 5 + b\\\\b = 6 - 5 = 1\\\\\text{So, the equation of the perpendicular line is }\\y = (5)/(3)x + 1`

This corresponds to Choice A