Question

Solve for X and Y with steps?

Answer 1

`\Large \boxed{\boxed{\textsf{$x=(47)/(7), y=15$}}}`

Explanation:

The shape inside the circle is a quadrilateral. The following property of circle geometry can be used to solve the problem:

`\large \boxed{\text{`

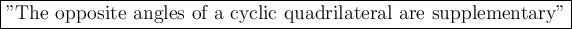
Proof:

Consider any quadrilateral, where the vertices touch on the circumference of a circle: ABCD, with origin O, as s

Required to prove: ∠ABC + ∠ADC = 180°

Let ∠AOC = 2x as shown in attached image.

∴ 2∠ABC = ∠AOC (using another property that "the perpendicular bisector of a chord passes through the circle's centre")

⇒ ∠ABC = x.

Now let ∠AOC = 2y.

Similarly, ∠ADC = y

⇒ ∠ABC + ∠ADC = x + y.

∵ It is clear that 2x + 2y = 360°,

⇒ x + y = 180°

∴∠ABC + ∠ADC = 180°, and hence statement is true.

Now, solving for x:

7x + 1 + 105° = 180

7x + 106 = 180

7x = 74

∴x = 74/7

Solving for y:

4y + 14 + 7y + 1 = 180

11y + 15 = 180

11y = 165

∴y = 15