Question

NO LINKS!!! URGENT HELP PLEASE!!

Edward opens a savings account with $250. The bank gives him an interest rate of 2.8% per year (simple interest). About how long will it take Edward to double his money? (SHOW WORK!!)

Equation: ___________________

Answer: __________________

Answer 1

Equation: 250(1 + 0.028t) = 500

Answer: 36 years

Explanation:

The equation we can use to solve this problem is the simple interest formula:

`\boxed{A = P (1 + rt)}`

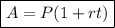
where:

• A is the amount of money in the account after t years.
• P is the principal (initial amount).
• r is the interest rate per year (as a decimal).
• t is the time in years.

Given the initial investment is $250 at an interest rate of 2.8%, and Edward wants to double his money:

• A = $500
• P = $250
• r = 0.028

Substite these values into the equation:

`500=250(1+0.028t)`

Swap sides:

`250(1+0.028t)=500`

Now solve for t:

`\implies (250(1+0.028t))/(250)=(500)/(250)`

`\implies 1+0.028t=2`

`\implies 1+0.028t-1=2-1`

`\implies 0.028t=1`

`\implies (0.028t)/(0.028)=(1)/(0.028)`

`\implies t=35.71428571...`

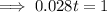
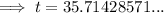
Assuming the interest is applied annually on the anniversary of the account opening, it will take Edward 36 years to double his money with a 2.8% simple interest rate.