Question

Complete the square to re-write the quadratic function in vertex form

Answer 1

to express the quadratic equetion in to factor form

you must use completing squere method

`y= {x}^(2) - 10x - 5`

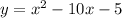
y + 5 = x2 - 10x

y + 5 = x2 - 10xy + 5 + 25 = x2 - 10x + 25

y + 5 = x2 - 10xy + 5 + 25 = x2 - 10x + 25y + 30 = (x - 5)2

y + 5 = x2 - 10xy + 5 + 25 = x2 - 10x + 25y + 30 = (x - 5)2 y = ( x - 5)2 - 30 so we get the factor form of the quadratic equetion.

In other way :

if you need to get vertex (5, -30)

or simply by (x, f(x)) which is (-b/2a,f(-b/2a)) form

a=1

a=1b=-10

a=1b=-10c=-5

so when u substitute and you will get (5, f(5))

then for the y-coordinate you substitute 5 in place of x and you will get -30 so vertex = (5, -30)