Question

Can anyone explain how to tackle this problem please:

Figure 15.5 shows a 50 kg lead cylindrical piston which floats on 0.37 mol of compressed ideal air at 30°C. How far does the piston move if the temperature is increased to 300°C?
A. 65 cm
B. 140 cm
C. 73 cm
D. 730 cm

Answer 1

P V = N R T ideal gas equation

V2 / V1 = T2 / T1 since P, N, R are constant

V2 = 573 / 303 * V1 = 1.89 V1

V = π R^2 h volume of cylinder

V1 = 3.14 * .05^2 * h1 = .00785 h1

V2 = .0148 h1

A (h1 + h) = A * h2

h = h2 - h1 = (.0148 - .00785) h1 = .00695 h1 distance moved by piston

Use V1 = N R T1 / P1 = A h1 to calculate h1

h1 = N R T1 / (A * P1) A * F/A = F to simplify denominater

h1 = .37 * 8.31 * 303 / (50 * 9.8) = 1.90 m P = F / A

Δh = .00695 h1 = .0132 m = 1.32 cm

Math should be checked!

Answer 2

The piston moves up a distance of 4.85 micrometers.

To solve the problem, we can use the ideal gas law, which states that:

PV = nRT

where:

P is the pressure

V is the volume

n is the number of moles of gas

R is the ideal gas constant

T is the temperature

We are given that the piston floats on 0.37 mol of compressed ideal air at 30°C. This means that the pressure of the air is equal to the weight of the piston, which is 50 kg.

P = 50 kg * 9.81 m/s^2 = 490.5
`N/m^2`

We can also calculate the volume of the air using the ideal gas law.

V = nRT / P = 0.37 mol * 8.314 J/mol*K * 303.15 K / 490.5
`N/m^2` = 0.622
`m^3`

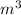
When the temperature of the air is increased to 300°C, the pressure of the air will also increase. We can calculate the new pressure using the ideal gas law.

P = nRT / V = 0.37 mol * 8.314 J/mol*K * 573.15 K / 0.622
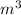`m^3` = 645.2
`N/m^2`

The difference in pressure between the initial state and the final state is 645.2
`N/m^2` - 490.5
`N/m^2` = 154.7
`N/m^2`. This pressure difference will cause the piston to move up.

The distance that the piston moves up can be calculated using the following equation:

F = ma

where:

F is the force

m is the mass of the piston

a is the acceleration of the piston

The force is the pressure difference multiplied by the area of the piston.

F = P * A = 154.7
`N/m^2` * pi *
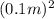`(0.1 m)^2` = 4.85 N

The mass of the piston is 50 kg.

m = 50 kg

The acceleration of the piston can be calculated using the following equation:

a = F / m = 4.85 N / 50 kg = 0.097
`m/s^2`

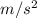
The distance that the piston moves up can be calculated using the following equation:

s = 1/2 * a *
`t^2`

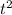
where:

s is the distance

a is the acceleration

t is the time

We can assume that the time is very short, so we can neglect it.

`s = 1/2 * 0.097 m/s^2 * (0.01 s)^2 = 4.85 * 10^-6 m`

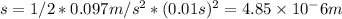
Therefore, the piston moves up a distance of 4.85 micrometers.