Question

The acceleration function (in m/s2) and the initial velocity v(0) are given for a particle moving along a line.

a(t) = 2t + 2, v(0) = −15, 0 ≤ t ≤ 5
Find the distance traveled during the given time interval.
I keep getting 25/3 but that is not correct :(

Answer 1

`(137)/(3)\approx 45.7\; \sf m`

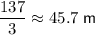
Explanation:

To find the velocity function, integrate the acceleration function (and add a constant of integration).

`\begin{aligned}\displaystyle v(t)=\int a(t) &= \int (2t + 2)\; \text{d}t\\\\&=\int 2t \; \text{d}t+\int 2\; \text{d}t\\\\&=(1)/(2) \cdot 2t^((1+1))+2t+\text{C}\\\\&=t^2+2t+\text{C}\end{aligned}`

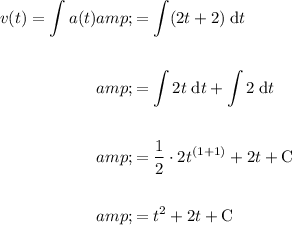
To find the constant of integration, C, substitute v(0) = -15 into the velocity function and solve for C:

`\begin{aligned}v(0)=(0)^2+2(0)+\text{C}&=-15\\0+0+\text{C}&=-15\\\text{C}&=-15\end{aligned}`

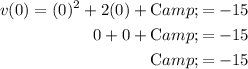
Therefore, the velocity function (in m/s) is:

`v(t)=t^2+2t-15`

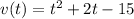
As we want to find the distance travelled during the given time interval 0 ≤ t ≤ 5, we first need to determine if the particle momentarily stops at any point in the given interval (and therefore changes direction). The particle will stop when its velocity is zero, so when v(t) = 0:

`\begin{aligned}v(t)&=0\\\implies t^2+2t-15&=0\\t^2+5t-3t-15&=0\\t(t+5)-3(t+5)&=0\\(t-3)(t+5)&=0\\\\\implies t&=3, -5\end{aligned}`

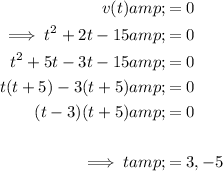
As time is positive only, the velocity is zero at t = 3 seconds.

Therefore, at t = 3, the particle changes direction and begins to move in the opposite direction. Therefore, the displacement between 0 ≤ t ≤ 5 consists of two parts: 0 ≤ t ≤ 3 and 3 ≤ t ≤ 5.

To find the distance travelled, first find the displacement function by integrating the velocity function:

`\begin{aligned}\displaystyle s(t)=\int v(t) &= \int (t^2+2t-15)\; \text{d}t\\\\&= \int t^2\; \text{d}t+\int 2t\; \text{d}t-\int 15\; \text{d}t\\\\&=(1)/(3)t^3+t^2-15t\left(+\text{C}\right) \end{aligned}`

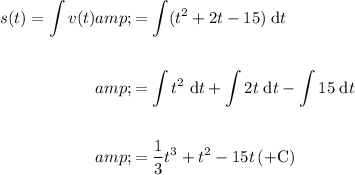
Distance is the absolute value of displacement.

As we want to find the distance travelled for the intervals 0 ≤ t ≤ 3 and 3 ≤ t ≤ 5, we need to add the absolute values of displacement for these intervals. So, the absolute values of the definite integrals for these intervals:

`\begin{aligned}\textsf{Distance}&=\left|\int^3_0 v(t)\right|+\left|\int^5_3 v(t)\right|\\\\&=\left|\left[(1)/(3)t^3+t^2-15t\right]^3_0\right|+\left|\left[(1)/(3)t^3+t^2-15t\right]^5_3\right|\\\\&=\left|\left((1)/(3)(3)^3+(3)^2-15(3)\right)-\left((1)/(3)(0)^3+(0)^2-15(0)\right)\right|+\\&\left|\left((1)/(3)(5)^3+(5)^2-15(5)\right)-\left((1)/(3)(3)^3+(3)^2-15(3)\right)\right|\\\\&=\left|(-27-0)\right|+\left|\left(-(25)/(3)-(-27)\right)\right|\end{aligned}`

`\begin{aligned}&=27+(56)/(3)\\\\&=(137)/(3)\end{aligned}`

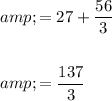
Therefore, the total distance travelled during the given time interval is 137/3 ≈ 45.7 meters.