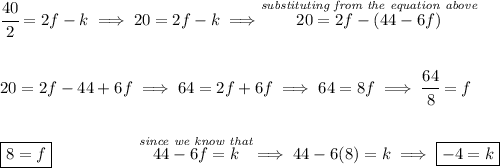Question

If the cubic polynomial -x³+fx²+kx - 62 is divided by (x-6) or (x+2),

the remainder in both cases is -14. Calculate the values of f and k.

Answer 1

so we know that the factors of (x-6) and (x+2) will yield a remainder of -14, thus by the remainder theorem we can say that the values of x = 6 and x = -2 will yield -14, that is for our function f(6) = f(-2) = -14, so let's plug those two values and see what we get for our "k" and "f"

`\boxed{x=6}\hspace{5em}f(6)=-x^3+fx^2+kx-62\\\\\\ -14=-(6)^3+f(6)^2+k(6)-62\implies -14=36f+6k-278 \\\\\\ 264=36f+6k\implies 264=6(6f+k)\implies \cfrac{264}{6}=6f+k \\\\\\ 44=6f+k\implies 44-6f=k \\\\[-0.35em] ~\dotfill\\\\ \boxed{x=-2}\hspace{5em} f(-2)=-x^3+fx^2+kx-62\\\\\\ -14=-(-2)^3+f(2)^2-k(2)-62\implies -14=8+4f-2k-62 \\\\\\ -14=4f-2k-54\implies 40=4f-2k\implies 40=2(2f-k)`

`\cfrac{40}{2}=2f-k \implies 20=2f-k\implies \stackrel{\textit{substituting from the equation above}}{20=2f-(44-6f)} \\\\\\ 20=2f-44+6f\implies 64=2f+6f\implies 64=8f\implies \cfrac{64}{8}=f \\\\\\ \boxed{8=f}\hspace{5em}\stackrel{\textit{since we know that}}{44-6f=k}\implies 44-6(8)=k\implies \boxed{-4=k}`