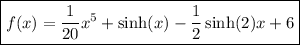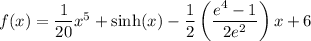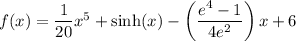Answer:
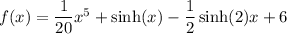
Explanation:
Given:
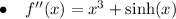
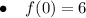
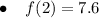
To find f'(x), integrate f''(x):
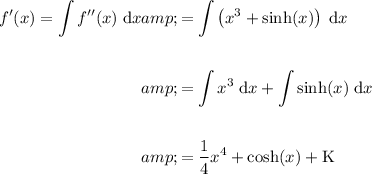
To find f(x), integrate f'(x):
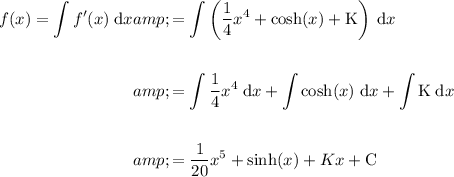
Substitute f(0) = 6 to determine the value of the constant C:

Substitute f(2) = 7.6 and C = 6 to determine the value of the constant K:
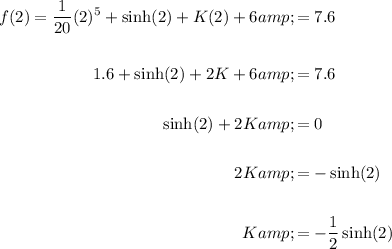
Therefore, function f(x) is: