Question

The present value of a bond that pays $60 in coupon payments at the end of each year for 3 years and an additional $1,200 at the end of the third year. If the interest rate is 7%, then the present value is $[blank]. Just enter a value. Round your final answer two decimal points. For example, 123.34 or 987.10.

Answer 1

The present value of the bond is $1,145.44.

Step-by-step explanation:

The present value of a bond can be calculated by discounting the future cash flows back to the present using the interest rate. In this case, the bond pays $60 in coupon payments at the end of each year for 3 years and an additional $1,200 at the end of the third year. The interest rate is 7%. To calculate the present value, we need to discount each cash flow using the interest rate:

1st year coupon payment =
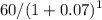`$60 / (1 + 0.07)^1` = $55.85

2nd year coupon payment =
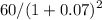`$60 / (1 + 0.07)^2` = $52.31

3rd year coupon payment + principal =
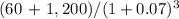`($60 + $1,200) / (1 + 0.07)^3` = $1,037.28

The present value is the sum of these discounted cash flows:

Present value = $55.85 + $52.31 + $1,037.28 = $1,145.44