Question

NO LINKS!! URGENT HELP PLEASE!!!

Determine the equation of the circle graphed below. Part 2c^2

Answer 1

Answer:
`(x+7)^2 + (y+1)^2 = 9`

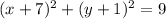
center = (-7, -1)

radius = 3

======================================================

Step-by-step explanation:

The highest point on the circle is at (-7,2)

The lowest point is at (-7, -4)

Connecting these endpoints gets us one diameter of this circle.

Apply the midpoint formula to these endpoints.

`\text{Endpoints: }(x_1,y_1) = (-7,2) \text{ and } (x_2,y_2) = (-7,-4)\\\\\text{Midpoint} = (x_m, y_m)\\\\\begin{array}l\cline{1-2}x_m = (x_1 + x_2)/(2) & y_m = (y_1 + y_2)/(2)\\ & \\x_m = (-7 +(-7))/(2) & y_m = (2 +(-4))/(2)\\ & \\x_m = (-14)/(2) & y_m = (-2)/(2)\\ & \\x_m = -7 & y_m = -1\\\cline{1-2}\end{array}\\\\\text{The midpoint is located at }(-7, -1)\\\\`

This midpoint of a diameter is also the location of the center of the circle. Recall that all diameters are a special type of chord that pass through the center of a circle.

The circle is centered at (-7, -1)

---------

Now compute the distance from the center (-7,-1) to a point on the circle's edge. Let's say we picked (-7,2)

The distance between these points is 3 units, which we can find by subtracting the y coordinates and using absolute value

distance = |2 -(-1)| = |2+1| = |3| = 3

You could use the distance formula, but it's probably easier to subtract and then use absolute value.

The distance of 3 units represents the radius of the circle. It's how far you need to go from the center to get to the circle's edge.

Circle radius = 3

---------

Summary

• (h,k) = (-7,-1) = center
• r = 3 = radius

We plug those items into the circle template equation.

`(x-h)^2 + (y-k)^2 = r^2\\\\(x-(-7))^2 + (y-(-1))^2 = 3^2\\\\(x+7)^2 + (y+1)^2 = 9`

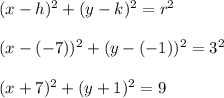
That last equation is the final answer.