Question

I do not get what a, b, c, and number 2 are asking. How do I write more equations when there are only one?? Please help.

Answer 1

Answers:

• problem 1, part (a)
  `3\text{x}+4y = 16\\`
• problem 1, part (b)
  `y = -(3)/(4)\text{x} + 4\\`
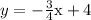
• problem 1, part (c)
  `y = -(1)/(4)\text{x} + 2\\`
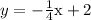
• problem 2,
  `y = (3)/(4)\text{x} +5\\`

Other answers are possible.

===================================================

Explanation for Problem 1, part (a)

We need to determine the equation of the line currently graphed.

That line goes through (0,4) and (4,1)

Use the slope formula on those two points.

`(x_1,y_1) = (0,4) \text{ and } (x_2,y_2) = (4,1)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (1 - 4)/(4 - 0)\\\\m = -(3)/(4)\\\\`

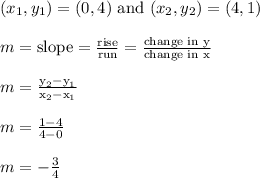
The slope is -3/4, which in decimal form is -0.75

I'll stick to the fraction form.

The graphed line has these two key important properties

• m = -3/4 = slope
• b = 4 = y intercept

So we go from
`y = m\text{x} + b` to
`y = -(3)/(4)\text{x} + 4`

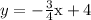
If we introduce a second equation that is exactly
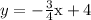`y = -(3)/(4)\text{x} + 4`, then this system

`\begin{cases}y = -(3)/(4)\text{x} + 4\\y = -(3)/(4)\text{x} + 4\\\end{cases}`

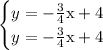
will have infinitely many solutions. They are the same line, so they overlap perfectly to share the same set of solution points.

Each solution is of the form (x,y) = (x, -0.75x+4) where x is any real number.

Let's rewrite that second equation so we appear to be a bit more creative.

I'll multiply both sides by 4 and then move the x term to the left side. This will get the equation into standard form Ax+By = C.

`y = -(3)/(4)\text{x} + 4\\\\4y = 4(-(3)/(4)\text{x} + 4)\\\\4y = -3\text{x} + 16\\\\3\text{x}+4y = 16\\`

Therefore this system

`\begin{cases}y = -(3)/(4)\text{x} + 4\\3\text{x}+4y = 16\\\end{cases}`

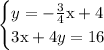
will have infinitely many solutions of the form (x,y) = (x, -0.75x+4)

Each solution is on the line shown in the graph that is given.

---------------------

Explanation for Problem 1, part (b)

The given graph has the equation
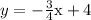`y = -(3)/(4)\text{x} + 4\\` as found in the previous part. The slope is -3/4 = -0.75

We want a parallel line to this, because parallel lines never cross which leads to "no solutions". So the answer will also have a slope of -3/4.

Parallel lines have equal slopes, but different y intercepts.

In this case, the y intercept is b = 1 due to the point (0,1)

We arrive at the answer
`y = -(3)/(4)\text{x} + 1\\`

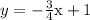
This system shown below has no solutions

`\begin{cases}y = -(3)/(4)\text{x} + 4\\y = -(3)/(4)\text{x} +1\\\end{cases}`

---------------------

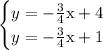
Explanation for Problem 1, part (c)

The new line must go through (0,2) and (4,1)

Compute the slope.

`(x_1,y_1) = (0,2) \text{ and } (x_2,y_2) = (4,1)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (1 - 2)/(4 - 0)\\\\m = -(1)/(4)\\\\`

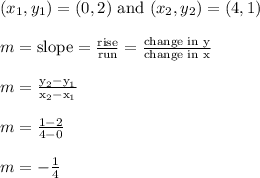
The slope is m = -1/4 and the y intercept is b = 2

We go from y = mx+b to
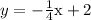`y = -(1)/(4)\text{x} + 2\\` which is the answer.

This system

`\begin{cases}y = -(3)/(4)\text{x} + 4\\y = -(1)/(4)\text{x} +2\\\end{cases}`

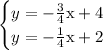
has one solution at (4,1) which is where the two lines cross.

---------------------

Explanation for Problem 2

The given equation of this system is
`y = (3)/(4)\text{x} - 4\\`

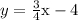
It has a slope of 3/4.

Anything parallel to this will also have the same slope. Refer to problem 1, part (b).

All we have to do is change the y intercept to something other than -4

Let's say we go for 5.

This system

`\begin{cases}y = (3)/(4)\text{x} - 4\\y = (3)/(4)\text{x} +5\\\end{cases}`

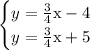
has no solutions.

You could use graphing software like GeoGebra or Desmos to confirm any of the answers mentioned earlier.