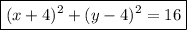Question

NO LINKS!! URGENT HELP PLEASE!!!!

Find an equation of the circle that satisfies the stated conditions. (Give your answer in standard notation.)

Tangent to both axes, center in the second quadrant, radius 4

Answer 1

`(x+4)^2+(y-4)^2=16`

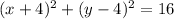
Explanation:

A tangent is a straight line that touches a circle at only one point.

Since the circle is tangent to both axes, and the center of the circle is in the second quadrant, the center of the circle lies on the line y = -x.

As the circle is tangent to the x-axis, the distance between the center of the circle and the x-axis is equal to the radius of the circle.

Similarly, as the circle is tangent to the y-axis, the distance between the center of the circle and the y-axis is also equal to the radius of the circle.

Therefore, the center of the circle will be 4 units to the left of the y-axis and 4 units up from the x-axis. Therefore, the coordinates of the center are (-4, 4).

`\boxed{\begin{minipage}{5 cm}\underline{Equation of a circle}\\\\$(x-h)^2+(y-k)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(h, k)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Substitute the center (-4, 4) and the radius, r = 4, into the standard equation of a circle:

`\implies (x - (-4))^2+(y-4)^2=4^2`

`\implies (x+4)^2+(y-4)^2=16`

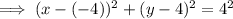
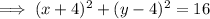
Therefore, the equation of the circle that satisfies the given conditions is:

`\boxed{(x+4)^2+(y-4)^2=16}`