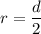Question

NEED help on questions 1-11 please!

Answer 1

Answer and Explanation:

The circumference of a circle is defined as:

`C = 2\pi r`

If we use 3.14 for π, then the formula becomes:

`C = 2(3.14)r`

`C = 6.28r`

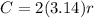
1

A regular polygon with 40 sides that is the same size as a circle will have a perimeter closer to the circumference of the circle than a polygon with 20 sides.

We can think of a circle as having infinite tiny sides, so the more sides a regular polygon has, the closer its circumference gets to a circle.

2

We can plug the given radius (
`r`) value into the above formula.

`C = 6.28(9 \text{ cm})`

`C \approx \boxed{56.6 \text{ cm}}`

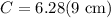
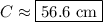
3

It's the same process as for problem 2.

`C = 6.28(9 \text{ in})`

`C \approx \boxed{150.7 \text{ in}}`

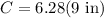
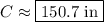
4

This time, we can take the original formula:
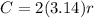`C = 2(3.14)r` and notice that
`2r = d`, so we can substitute the given diameter (
`d`) value for
`2r` in that formula.

`C = 3.14d`

`C = 3.14(14.22 \text{ mm})`

`C \approx \boxed{44.7 \text{ mm}}`

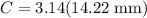
5

This problem is the same as problems 1 and 2, but it's in word problem format. We can keep plugging into the circumference formula.

`C = 6.28(9 \text{ in})`

`C \approx \boxed{56.5 \text{ in}}`

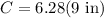
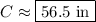
6 and 7

These are equivalent to problem 4, but in word problem format. Keep plugging into the formula
`C = 3.14d`.

__________

The area of a circle is defined as:

`A = \pi r^2`

But we can plug in 3.14 for π:

`A = 3.14r^2`

__________

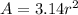
8

We can plug the given radius value into the above area formula.

`A = 3.14(7 \text{ yd})`

`A \approx \boxed{21.98 \text{ yd}}`

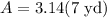
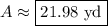
9, 10, and 11

These are the same type of problem as 8, but since we are given the diameter (
`d`), we have to divide it by 2 to plug it in for the radius (
`r`).

`r = (d)/(2)`