Question

This is for trigonometry and I have to find X then round to the nearest tenth

Answer 1

x = 1.5 m

Explanation:

We have been given a right triangle where the side opposite the angle 50° is 1.8 m and the side adjacent the angle 50° is labelled x.

To find x, use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

Substitute θ = 50°, O = 1.8 m and A = x into the equation:

`\implies \tan 50^(\circ) = (1.8)/(x)`

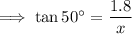
To solve for x, multiply both sides by x:

`\implies x \cdot \tan 50^(\circ) = x \cdot (1.8)/(x)`

`\implies x \tan 50^(\circ) =1.8`

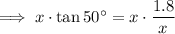
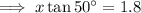
Divide both sides by tan 50°:

`\implies (x \tan 50^(\circ))/(\tan 50^(\circ)) =(1.8)/(\tan 50^(\circ))`

`\implies x=(1.8)/(\tan 50^(\circ))`

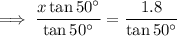
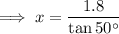
Using a calculator:

`\implies x = 1.51037933...`

`\implies x = 1.5\; \sf m\;(nearest\;tenth)`

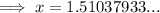
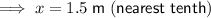
Therefore, the length of side x is 1.5 meters when rounded to the nearest tenth.