Question

4. 1. 33% of 2406 adults surveyed said that skim milk is a good calcium source. Find the margin of error and explain the results

Answer 1

To find the margin of error, we use the formula:

Margin of Error (ME) = Z *
`√((p * (1-p) / n))`

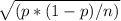
Z = 1.96 (for a 95% confidence level)

p = 0.33 (proportion of adults who said skim milk is a good calcium source)

(1-p) = 1 - 0.33 = 0.67 (complement of the estimated proportion)

n = 2406 (sample size)

ME = 1.96 *
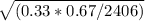`√((0.33 * 0.67 / 2406))` = 0.0185 (rounded to four decimal places)

This means that we can estimate, with 95% confidence, that the true proportion of adults who believe skim milk is a good calcium source falls within a range that is 1.85% above or below the reported proportion of 33% based on the survey results.

In other words, the actual proportion of adults who believe skim milk is a good calcium source could be as low as 31.15% or as high as 34.85% based on the margin of error.