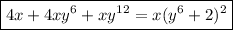Write as a product: 4x+4xy^6+xy^12

Question

asked Nov 23, 2024 207k views

1 Answer

Gfernandes · Answer 1 · 2024-11-27T05:19:59+0000

Answer:

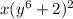
x(y^6+2)^2

Explanation:

Given polynomial expression:

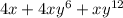
4x+4xy^6+xy^(12)

Factor out the common term x:

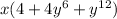
x(4+4y^6+y^(12))

Now factor (4 + 4y⁶ + y¹²).

Rewrite the exponent 12 as 6·2:

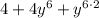
$4+4y^6+y^(6 \cdot 2)$

$\textsf{Apply the exponent rule:} \quad a^(bc)=(a^b)^c$

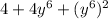
4+4y^6+(y^6)^2

Rearrange to standard form:

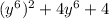
(y^6)^2+4y^6+4

Rewrite 4y⁶ as 2·2·y⁶ and 4 as 2²:

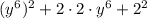
$(y^6)^2+2\cdot2\cdot y^6+2^2$

$\textsf{Apply\;the\;Perfect\;Square\;formula:}\quad a^2+2ab+b^2=(a+b)^2$

Therefore, a = y⁶ and b = 2:

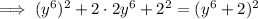
$\implies (y^6)^2+2\cdot2y^6+2^2=(y^6+2)^2$

Therefore, the given polynomial expression can be written as a product of two factors, x and (y⁶ + 2)²:

$\boxed{4x+4xy^6+xy^(12)=x(y^6+2)^2}$