Question

Find two consecutive integers whose sum of their squares is 702 ASAP!!

Answer 1

Answer: No solutions

Explanation:

Let n be the smallest of the two consecutive integers. Then n must satisfy the equation
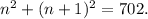`n^2+(n+1)^2=702.` After expanding the second term, we get

`n^2+(n+1)^2=702\\\implies n^2+n^2+2n+1=702\\\implies 2n^2+2n+1=702\\\implies 2n^2+2n-701=0.`

But the quadratic formula doesn't give any integer solutions, so there are no such integers n.