Answer:
A and B
Explanation:
Let's factor this the "old fashioned" way. The standard form of a quadratic is

If you're familiar with the quadratic formula I'd say throw it into that, but if not, again, let's do it the "old fashioned" way.
We need to find the product of our a and c. Our a = 2 and our c = -3. So that gives us a -6. Now we have to find the factors of 6 (the negative right now doesn't matter so much). The factors of 6 are 1, 6 and 2, 3. Both of those possibilities will work to give us a +5, which is the linear term. Putting in the 2, 3 first:
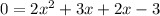
Now group the terms together into groups of 2:
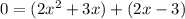
The idea is to factor out something common in each term so that what's left over in the parenthesis in both terms is exactly the same. In the first term we can factor out a common x, and in the second term, the only thing common is a 1. So that looks like this:
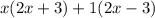
What's inside those parenthesis are not actually identical, so 2 and 3 won't work. Lets try 1 and 6. For those 2 numbers to equal a +5, the 6 is positive and the 1 is negative. So let's try that:

In the first term we can factor out the common 2x and in the second term we can factor out the common -1:
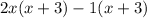
Now what's common is
 , so we can factor THAT out and what is left over is
, so we can factor THAT out and what is left over is
 :
:

If
 , then
, then
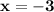
and if
 , then
, then
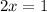 and
and
