Question

Circle Q is centered at Q(-2, 1) with a diameter

Does P(0.5, 7) lie on circle Q?
yes or no

Answer 1

• Yes , the point lies on the circle.

Explanation:

To find:-

• If point (0.5 , 7) lies on the circle Q .

Answer:-

We are here given that the diameter of the circle is 13 and its centre is (-2,1) . As we know that radius is half of diameter , hence the radius of the circle would be,

`\longrightarrow r =(d)/(2)=(13)/(2)=\boxed{6.5} \\` .

Now if the given point (0.5,7) lies on the circle, then it's distance from the centre would be equal to the radius of the circle . We can calculate the distance between two points using the distance formula . The distance formula is,

Distance formula:-

`\longrightarrow\boxed{\boldsymbol{ d =√((x_2-x_1)^2+(y_2-y_1)^2)}} \\`

Here we need to find out the distance between (-2,1) which is the centre and (0.5,7) . So on substituting the respective values, we have;

`\longrightarrow d =√( ( -2-0.5)^2+(7-1)^2)\\`

`\longrightarrow d = √( (-2.5)^2 + (6)^2)\\`

`\longrightarrow d =√(6.25 + 36 ) \\`

`\longrightarrow d = √( 42.25)=√((6.5)^2) \\`

`\longrightarrow d = 6.5 \\`

Hence here we conclude that ,

`\longrightarrow \boxed{\boldsymbol{ d = r }}\\`

Hence the point (0.5,7) lies on the circle .

Answer 2

Yes, point P(0.5, 7) lies on circle Q.

Explanation:

To determine if point P lies on circle Q, first create an equation for circle Q using the equation of a circle formula.

`\boxed{\begin{minipage}{5 cm}\underline{Equation of a circle}\\\\$(x-h)^2+(y-k)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(h, k)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

The diameter of a circle is twice its radius.

Therefore, the radius of circle Q is:

`\implies r=(d)/(2)=(13)/(2)=6.5`

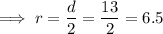
Given the center is (-2, 1) and the radius is 6.5, substitute these values into the equation of a circle formula to create an equation for circle Q:

`\implies (x-(-2))^2+(y-1)^2=6.5^2`

`\implies (x+2)^2+(y-1)^2=42.25`

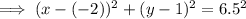
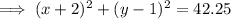
To determine if point P(0.5, 7) lies on circle Q, substitute x = 0.5 and y = 7 into the equation of circle Q. If it equals 42.25, the point lies on the circle.

`\begin{aligned}\implies (0.5+2)^2+(7-1)^2&=(2.5)^2+(6)^2\\&=6.25+36\\&=42.25\end{aligned}`

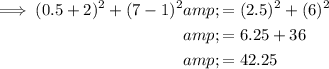
Therefore, point P(0.5, 7) does lie on circle Q.