Question

The length of a rectangular flower bed is 3 ft less than twice its width. The area of the bed is 54 ft2. What are the dimensions of the flower bed.

Answer 1

w = 6 ft.; l = 9 ft.

Explanation:

We know that the formula for area of a rectangle is A = lw, where l is the length and w is the width.

Because we're told that the length of the flower bed is 3 ft less than twice its width, we have l = 2w - 3

To find the length and width, can plug in 54 into the equation and substitute our formula for length into the equation.

This gives us 54 = (2w - 3)*w

If we rewrite the equation, we'll see that its quadratic:

`54=(2w-3)w\\54=2w^2-3w\\0=2w^2-3w-54`

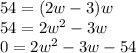
Now, we can first solve for width using the quadratic formula, which yields a positive and negative solution.

(For the sake of the quadratic equation, 0= ax^2 + bx + c is the standard form of quadratic equation and in our equation 2 is a, -3 is b, and -54 is c)

Positive:

`x=(-b+√(b^2-4ac) )/(2a) \\\\w=(-(-3)+√((-3)^2-4(2)(-54)) ))/(2(2))\\ \\w=(3+√(441) )/(4)\\ \\w=(3+21)/(4)\\ \\w=(24)/(4)\\\\w=6`

Negative:

`x=(-b-√(b^2-4ac) )/(2a) \\\\w=(-(-3)-√((-3)^2-4(2)(-54)) ))/(2(2))\\ \\w=(3-√(441) )/(4)\\ \\w=(3-21)/(4)\\ \\w=(-18)/(4)\\\\w=-4.5`

We know that we can't have a negative measure, so the width is 6 ft.

Twice the width is 12 (6 * 2) and 3 less than this is 9 (12 - 3), so the length is 9 ft.