Question

I'm extremely stuck on this question, I know it's not C but yeah if you can figure it out I would love that!

Answer 1

Answer: Choice D

`\displaystyle (ac)/(2) - (\pi b^2)/(8)\\\\`

=============================================

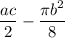
Work Shown:

`\text{area of a triangle} = \frac{\text{base}*\text{height}}{2}\\\\\text{area of a triangle} = (ac)/(2)\\\\`

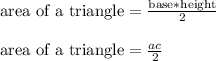
The semicircle has diameter b. The radius is b/2, (1/2)*b, or 0.5b

`\text{area of a semicircle} = 0.5*(\text{area of a circle})\\\\\text{area of a semicircle} = 0.5*\pi*r^2\\\\\text{area of a semicircle} = 0.5*\pi*(0.5b)^2\\\\\text{area of a semicircle} = 0.5*\pi*0.25b^2\\\\\text{area of a semicircle} = 0.5*0.25*\pi*b^2\\\\\text{area of a semicircle} = 0.125*\pi*b^2\\\\\text{area of a semicircle} = (1)/(8)*\pi b^2\\\\\text{area of a semicircle} = (\pi b^2)/(8)\\\\`

We subtract the area of the triangle and the semicircle to determine the area of the blue region.

`\text{blue region} = \text{triangle area} - \text{semicircle area}\\\\\text{blue region} = (ac)/(2) - (\pi b^2)/(8)\\\\`

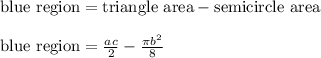
Therefore, choice D is the final answer