Question

A chain fits tightly around two gears as shown. The distance between the centers of the gears is 32 inches. The radius of the larger gear is 19 inches. Find the radius of the smaller gear. Round your answer to the nearest tenth, if necessary. The diagram is not to scale.

Answer 1

The answer to your problem is, C.

Explanation:

From the given figure it is noticed that the radius of a circle is 11 inches and the centers of two circles are 20 inches apart. The length of the direct common tangent between both circles is 19 inches.

If the centers of two circles of radius r₁ and r₂ are d units apart, then the length of the direct common tangent between them is

`L = \sqrt{d^(2) - (r_(1) - r_(2) )^(2) }`

`19 = \sqrt{20^(2) - (11-r_(2) )^(2) }`

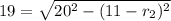
Next, Square both sides.

`361 = 400 - ( 11 - r_(2) )`

`( 11 - r_(2) )^(2) = 400 - 361`

`( 11 - r_(2) )^(2) = 39`

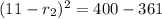
Change the square root both sides.

`11-r = √(39)`

`11- 6.245 = r`

`4.775 = r`

`R = 4.8ish`

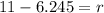
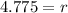
Therefore the radius of second circle is 4.8 inches

Thus the answer to your problem is, C.