Question

A ship's sonar locates a treasure chest below the water at a 22 degree angle of depression. A diver is then lowered 30 meters to the ocean floor. How far is the diver to the treasure? Round answer to the nearest hundredth (two decimal places)

Answer 1

The horizontal distance between the diver and the treasure is 74.25 meters (to two decimal places).

Explanation:

Angle of Depression

The angle of depression is the angle between a horizontal line of sight and the line of sight from an observer to an object that is located below the observer.

To find how far the diver is to the treasure, model the scenario as a right triangle.

If the angle of depression is 22°, this is the angle formed by the hypotenuse and the horizontal leg of the right triangle. If the diver is lowered 30 m to the ocean floor, the side opposite the angle is 30 m. (See attachment).

The distance between the diver and the treasure is the side adjacent to the angle, so we can find this by using the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

Given:

• θ = 22°
• O = 30 m
• A = x m

Substitute these values into the ratio and solve for x:

`\implies \tan 22^(\circ)=(30)/(x)`

`\implies x=(30)/(\tan 22^(\circ))`

`\implies x=74.25260...`

`\implies x=74.25\; \sf m\;(2\;d.p.)`

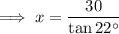
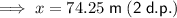
Therefore, the horizontal distance between the diver and the treasure is 74.25 meters (to two decimal places).