Question

Solve the following simultaneous equations using an algebraic method.

4x - 7y = 15
5x - 2y = 12

Answer 1

(x, y) = (2, -1)

Explanation:

You want to solve this system of equations using an algebraic method:

• 4x -7y = 15
• 5x -2y = 12

Cross multiplication method

Writing these equations in general form and making an array of coefficients with the x-coefficient repeated, we get the equations and array ...

• 4x -7y -15 = 0
• 5x -2y -12 = 0

`\begin{array}{cccc}4&-7&-15&4\\5&-2&-12&5\end{array}`

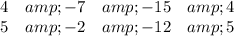
Working from the left calculating determinants of pairs of columns, we have ...

∆ = 4(-2) -5(-7) = 27

∆x = -7(-12) -(-2)(-15) = 54

∆y = -15(5) -(-12)(4) = -27

The variable values are ...

x = ∆x/∆ = 54/27 = 2

y = ∆y/∆ = -27/27 = -1

The solution is (x, y) = (2, -1).

__

Additional comment

The graph confirms this solution.

The "cross multiplication method" is useful when the coefficients are such that elimination or substitution involves more arithmetic operations than the minimum. The amount of math involved in calculating the x- and y-values is on par with what would be required for "elimination." The method is substantially equivalent to "Cramer's Rule."

Answer 2

4x −7y=21

x+2y=99

Explanation

4x - 7y = 15

5x - 2y = 12

First equation times 2:

8x - 14y = 30

Second equation times 7:

35x - 14y = 84

Subtract,

27x = 54

x = 54/27 = 2

2y = 5x - 12 = 10 - 12 = -2

y = -1

Answer: x=2, y = -1

Check:

4(2)-7(-1)=8+7=15, good

5(2) -2(-1) = 10 + 2 = 12, good

ax + by = c

dx + ey = f

has solutions

x = (ce-bf)/(ae-bd), y = (a f-cd)/(ae-bd)

4x - 7y = 15

5x - 2y = 12

has solutions

denom = ae-bd = 4(-2) - (-7)(5) = 27

x = (15(-2) - (-7)(12))/27 = (-30 + 84)/27 = 2

y = (4(12)-15(5))/27 = (48-75)/27 = -27/27 = -1