Question

I need a bit of help with this, as well as how to solve these situations, thanks in advance.

Answer 1

x = 32°

Explanation:

The definition of tangent means that the angle formed by the line and the circle is a 90° angle. We can also see that the two segments connected to the center have equal angles because they are both radii of the circle. They form a triangle and the angle measurements are 61°, 61° and 58°. We have two angle measurements of the overall triangle, 58°, 90° (from the tangent), and x°.

The sum of the angles of any triangle is 180°. Therefore, we can form an equation to calculate the value of x.

58 + 90 + x = 180

x = 180 - 90 - 58

x = 32°

Answer 2

x = 32°

Explanation:

To find:-

• The value of "x" .

Answer:-

As we know that angle made by tangent on the centre is a right angle . So here
`\angle`OBC will be 90° ( as CB is tangent on the circle.) Again we know that the angles opposite to equal sides are equal . Therefore here OB and OA are radii of the circle which are equal. So we can say that;

`\sf:\implies \red{ \angle OBA = \angle OAB = 61^o}\\`

Again we know that the angle sum property of a triangle is 180° . Therefore in ∆OBA ,

`\sf:\implies 61^o + 61^o + \angle AOB = 180^o \\`

`\sf:\implies 122^o + \angle AOB = 180^o \\`

`\sf:\implies \angle AOB = 180^o - 122^o \\`

`\sf:\implies \angle AOB = 58^o\\`

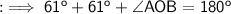
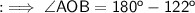
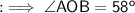
Finally look into the ∆OBC ,

`\sf:\implies \angle BOC + \angle OCB + \angle CBO = 180^o\\`

`\sf:\implies 58^o + 90^o + x = 180^o \\`

`\sf:\implies 148^o + x = 180^o \\`

`\sf:\implies x = 180^o - 148^o \\`

`\sf:\implies \red{ x = 32^o }\\`

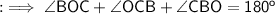
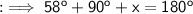
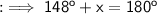
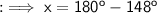
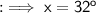
Hence the value of x is 32°.