Question

Can someone please explain and answer this for me I’m so lost

Answer 1

`\left(\begin{array}{cc}0&24\\13&27\end{array}\right)`

Explanation:

I will attempt to explain using the following example. Let us consider the product (multiplication) of the following matrices:

`\left(\begin{array}{cc}a_(1,1)&a_(1,2)\\a_(2,1)&a_(2,2)\end{array}\right) \cdot \left(\begin{array}{cc}b_(1,1)&b_(1,2)\\b_(2,1)&b_(2,2)\end{array}\right) = \left(\begin{array}{cc}c_(1,1)=c_(1* 1)&c_(1,2)=c_(1*2)\\c_(2,1)=c_(2*1)&c_(1,2)=c_(2*2)\end{array}\right)`

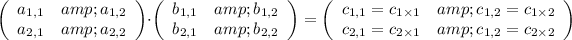
Note that the first number in each coefficient refers to the row number, while the second number refers to the column number.

Then
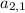`a_(2,1)` indicates the element in the second row and first column.

To calculate the product of two matrices, we need to multiply each row of the first matrix by each column of the second matrix.

Example:

`c_(1,1)= (a_(1,1) \cdot b_(1,1) + a_(1,2) \cdot b_(2,1))`

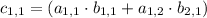
Now, we can apply this to the original exercise:

`\left(\begin{array}{cc}5&-2\\4&1\end{array}\right) \left(\begin{array}{cc}2&6\\5&3\end{array}\right) =\left(\begin{array}{cc}c_(1,1)&c_(1,2)\\c_(2,1)&c_(2,2)\end{array}\right)`

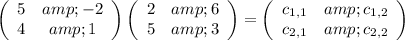
Next, we will calculate each value of c using the multiplication process we just discussed.

`c_(1,1)= (5(2)+-2(5)) = 10-10 =0\\c_(1,2)= (5(6)+-2(3)) = 30-6 =24\\c_(2,1)= (4(2)+1(5)) = 8+5 =13\\c_(2,2)= (4(6)+1(3)) = 24+3 =27\\`

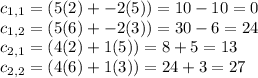
Thus, we have obtained the final result of the matrix product:

`\left(\begin{array}{cc}5&-2\\4&1\end{array}\right) \left(\begin{array}{cc}2&6\\5&3\end{array}\right) =\left(\begin{array}{cc}0&24\\13&27\end{array}\right)`

`\text{-B$\mathfrak{randon}$VN}`