Answer:
20) y = 3/4x + 3 1/2
21) Parallel: y = 3/4 x - 2 3/4
Perpendicular: y =
 x + 7
x + 7

Explanation:
20)
y = mx + b
y = __x + ___ We need to find the slope that the y-intercept. We are given the slope 3/4. We will you the x and y values from the point (2,5) to find the y intercept. Use 5 for y and 2 for x
y = mx + b
5 = 2(3/4) + b
5 = 3/2 + b Subtract 3/2 from both sides
5 - 3/2 = 3/2 -3/2 +b
 -
-
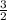 = b
= b
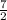 or 3
or 3

y = 3/4x + 3 1/2
21)
Parallel slopes are equal so the slope will be 3/4. Now we will use the x and y values from the point (5,1) to find the y-intercept. We will use 1for y and 5 for x
y = mx + b
1 = 5(3/4) +b
1 = 15/4 + b Subtract 15/4 from both sides.
 -
-
 =
=
 -
-
 + b
+ b
 or - 2
or - 2
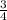
y = 3/4 x - 2 3/4
Perpendicular slopes or the opposite reciprocals. So the slope of the reciprocal equations would be
 . We would still use the x and y values from the point (5,1)
. We would still use the x and y values from the point (5,1)
1 = -4/3(5) + b
1 =
 + b Add 20/3 to both sides
+ b Add 20/3 to both sides
 +
+
 =
=
 +
+
 + b
+ b
 or 7 2/3
or 7 2/3
y =
 x + 7
x + 7

Helping in the name of Jesus.