Answer:

Explanation:
We are given a right angled triangle, with two sides as 4.9 and 8 . And we are interested in finding out the measure of the angle "x" . With respect to angle x , the side measuring 8 is perpendicular and that measuring 4.9 is base.
In a right angled triangle, tangent is defined as the ratio of perpendicular and base .
So , according to the question,
Now we have;
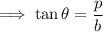
Here the angle is " x " , so that ,
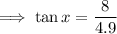
Simplify,
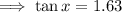
Take arctan on both the sides,
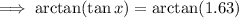
Simplify,


Hence the value of x is 59.2° .