Question

Which of the following equation represents a line that passes through the points (-8,-19) and (10,8)

Answer 1

`y-8=(3)/(2)(x-10)`

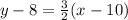
Explanation:

Before we can do anything first thing we need to do is find the slope.

We can do this given two points by using the formula
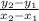`(y_2-y_1)/(x_2-x_1)` where all of the numbers used in this formula are points on the line in accordance to (x,y)

Plug in the values

`(8-(-19))/(10-(-8))`

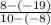
Evaluate, don't forget to simplify

`(27)/(18) =(3)/(2)`

Now that we have the slope of the line, all we have to do is write an equation of the line. This means we can write it in

Slope intercept form:
`y=mx+b`

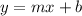
Point slope form:
`y-y_1 =m(x-x_1)`

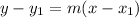
We will use point slope form since its easier. The easier point to use is (10,8), so we will use that as y1 and x1.

`y-8=(3)/(2)(x-10)`

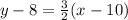
And that is our equation of the line!

Answer 2

To find the equation of a line that passes through two points, we can use the slope-intercept form, which is y = mx + b, where m is the slope and b is the y-intercept. First, let's calculate the slope (m):

m = (y2 - y1) / (x2 - x1)

Using the given points, (-8, -19) and (10, 8):

m = (8 - (-19)) / (10 - (-8)) = (27) / (18) = 3 / 2

Now that we have the slope, we can use one of the points to find the y-intercept (b). Let's use the point (-8, -19):

-19 = (3/2)(-8) + b

-19 = -12 + b

b = -7

Now that we have both the slope (m) and the y-intercept (b), we can write the equation of the line in slope-intercept form:

y = (3/2)x - 7