Question

Determine if the statement is True or False. (a) The volume of a solid can be computed by either a double integral or a triple integral True O False (b) If W is the sphere of radius 1 centered at the origin and W1 is the portion of W in the first octant, then fdA = 식 f dA True False

Answer 1

a) The first statement is true, you can find volumes with these integrals.

b) The second statement is false, we can define the equality:

`(1/8)\int\limits_W {f} \, dA = \int\limits_(W_1) {f} \, dA`

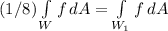
Are the claims true or false?

a) Double integrals: These are suitable for calculating the volume of simpler solids where one dimension can be treated as fixed (like a cylinder or a cone). In such cases, we integrate over the remaining two dimensions to find the total volume.

Triple integrals: These are more general and can be used to find the volume of any solid shape, regardless of its complexity. We integrate over all three dimensions in space to encompass the entire volume of the solid.

Therefore, while both types of integrals can be used to find volume, their applicability depends on the specific shape of the solid and the level of complexity involved.

b) If W is the sphere of radius 1 centered at the origin and W1 is the portion of W in the first octant, then:

`(1/8)\int\limits_W {f} \, dA = \int\limits_(W_1) {f} \, dA`

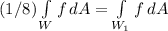
So integrating over W1 is equivalent to integrating over one-egith of W.