Question

I need help on this question!

Answer 1

The expression for the area of the shaded region is:

`5x^2+7x-26`

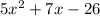
Explanation:

The area of the shaded region of the given figure can be calculated by subtracting the area of the unshaded inner rectangle from the area of the outer rectangle.

The area of a rectangle is the product of its width and length:

`\boxed{A=w \cdot l}`

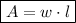
Therefore, the area of the inner (unshaded) rectangle is:

`\begin{aligned}\sf Area_(inner)&=(x-3)(x-6)\\&=x^2-6x-3x+18\\&=x^2-9x+18\end{aligned}`

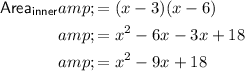
The area of the outer rectangle is:

`\begin{aligned}\sf Area_(outer)&=(2x+2)(3x-4)\\&=6x^2-8x+6x-8\\&=6x^2-2x-8\end{aligned}`

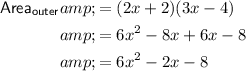
Therefore, the area of the shaded region is:

`\begin{aligned}\sf Area_(shaded\;region)&=\sf Area_(outer)-Area_(inner)\\&=(6x^2-2x-8)-(x^2-9x+18)\\&=6x^2-2x-8-x^2+9x-18\\&=6x^2-x^2+9x-2x-8-18\\&=5x^2+7x-26\end{aligned}`