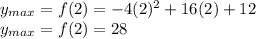Question

What is the maximum value of f(x)=-4x^2+16x+12 ?

Answer 1

Max = 28

Explanation:

The equation given is in the standard form of a qudaratic equation, which is:

`y = ax^2+bx+c`

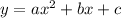
The max value is the y-coordinate of the maximum and we can find it using the formula

`x_(max)=-(b)/(2a)\\\\ y_(max)=a(-(b)/(2a))^2+b(-(b)/(2a))+c`

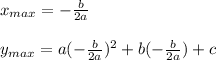
As the formula shows, -b/2a yields the x-coordinate of the vertex (a maxiumum in this problem). Then we allow this value to become the input of the quadratic function which yields the y-coordinate of the max and ultimately the maximum value:

Since 16 is b and -4 is a in our equation, we plug this in first to find the x-coordinate of the max:

`x_(max)=-(16)/(2(-4))\\ x_(max)=(-16)/(-8)\\ x_(max)=2`

Since 2 is the x-coordinate of the maximum, we can now plug this in to yield the y-coordinate of the maximum (aka the max value):

`y_(max)= f(2)=-4(2)^2+16(2)+12\\y_(max)=f(2)=28`