Question

HELP ON GEOMETRY

Given Line M is parallel to line N

Prove: angle 1 is supplementary to angle 3

Answer 1

R2. If parallel lines are cut by a transversal, then corresponding angles are congruent.

R3. Definition of congruent angles.

R5. Linear Pair Theorem. Two angles that form a linear pair are supplementary.

S7. m<1 + m<3 =180°

S8. <1 is supplementary to <3

Answer 2

Given parallel lines M and N, angles 1 and 3 are supplementary. Angle 2 equals 12 (vertical angles). Corresponding angles equality (m1 = m2) leads to the proof through linear pair and substitution properties.

Given: Line M is parallel to line N.

To prove: Angle 1
`(\(\angle 1\))` is supplementary to angle 3
`(\(\angle 3\)).`

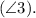
Given: Line M is parallel to line N.

Vertical angles are congruent:
`\(\angle 2 = 12\)`. When two lines intersect, opposite angles (vertical angles) formed are equal.

Corresponding angles of parallel lines are congruent:
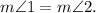`\(m\angle 1 = m\angle 2\).` When a line is parallel to another line, corresponding angles are equal.

Definition of a linear pair:
`\(\angle 2\)` and
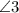`\(\angle 3\)` form a linear pair. A linear pair consists of two adjacent angles whose measures add up to 18

Linear pair angles sum to 180°:**
`\(m\angle 2 + m\angle 3 = 180°\).`

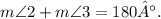
Substitution property of equality:** Since
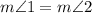`\(m\angle 1 = m\angle 2\)`, we substitute
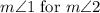`\(m\angle 1\) for \(m\angle 2\)` in the equation:
`\(m\angle 1 + m\angle 3 = 180°\).`

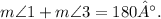
Definition of supplementary angles:** Angle 1
`(\(\angle 1\))` and angle 3
`(\(\angle 3\))` are supplementary when their measures add up to 180°.

So, through the given information about parallel lines and angle relationships, we've shown that
`\(m\angle 1 + m\angle 3 = 180°\),` which proves that angle 1
`(\(\angle 1\))`is supplementary to angle 3
`(\(\angle 3\))`.