The equation of the line that best fits the data, obtained using the least squares method is;
 ≈ 0.03478·x + 5.7838
≈ 0.03478·x + 5.7838
The steps used to find the best fit line equation is presented as follows;
The values in the table can be presented as follows;
X | Y
50 10
110 10
230 10
660 30
720 30
970 40
The least squares method equation can be used to find the slope-intercept of the equation of the line that best fits the data as follows;
The equation of the line in slope-intercept form, using the least squared method is;
 = m·x + c
= m·x + c
Where;
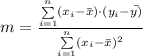
c =
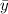 - m·
- m·

The data in the dable can be evaluated using MS Excel to get;
 ≈ 456.6667
≈ 456.6667
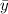 ≈ 21.66667
≈ 21.66667
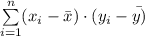 = 24733.33
= 24733.33
 = 711133.3
= 711133.3
Therefore;
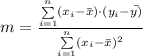 = 24733.33/711133.3
= 24733.33/711133.3
24733.33/711133.3 ≈ 0.03478
m ≈ 0.03478
c ≈ 21.66667 - 0.03478 × 456.6667
c ≈ 5.7838
The equation of the best fit line is therefore;
 ≈ 0.03478·x + 5.7838
≈ 0.03478·x + 5.7838