Question

Correct!

Correct Answer
A cylindrical capacitor is made of two thin-walled concentric
cylinders. The inner cylinder has radius Ra = 7.2 mm, and the outer
one a radius R = 15 mm. The region between the cylinders
contains a dielectric with constant k =2.6. The common length of
the cylinders is L=4.4 m (Assume the cylinders can be treated as
ideal infinite cylinders.)
Determine the potential energy stored in this capacitor when a
potential difference V=27.5V is applied between the inner and
outer cylinders in nJ.
327.722
327.8707 margin of error +/-1%

Could you show all work look for correct answer

Answer 1

The capacitor's potential energy depends on its geometry, dielectric properties, and applied voltage. Using these factors, we can calculate the stored energy, which in this case is approximately 327.7 microjoules.

The potential energy stored in the capacitor is due to the electric field created by the potential difference (voltage) between the inner and outer cylinders. This field is influenced by the dimensions of the cylinders, the dielectric constant, and the applied voltage.

Steps to solve:

Capacitance: Calculate the capacitance using the formula for a cylindrical capacitor with a dielectric:

C = (2 * π * ε * k * L) / ln(R/Ra)

where:

ε is the permittivity of free space (8.854 x
`10^{-12` F/m)

k is the dielectric constant (2.6)

L is the length of the cylinders (4.4 m)

R is the outer cylinder radius (15 mm)

Ra is the inner cylinder radius (7.2 mm)

Potential Energy: Calculate the potential energy stored using the formula:

U = 1/2 * C *
`V^2`

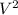
where:

C is the capacitance calculated in step 1

V is the applied voltage (27.5 V)

Answer:

Plugging in the values, you get:

U ≈ 327.7 μJ

The capacitor's potential energy depends on its geometry, dielectric properties, and applied voltage. Using these factors, we can calculate the stored energy, which in this case is approximately 327.7 microjoules.