Question

Max is drawing plans for a garden, measured in feet, which is shown below on the coordinate plane. Max has two vertices of the garden at points (Negative 1, 2) and (Negative 1, Negative 2). On a coordinate plane, points (negative 1, 2) and (negative 1, negative 2) are plotted. At which points should Max have the other two vertices in order to make the area of his garden 20 square feet? (2, Negative 2) and (2, 2) (4, Negative 2) and (4, 2) (3, Negative 2) and (3, 2) (5, Negative 2) and (5, 2)

Answer 1

Max should have the other two vertices at (4, 2) and (4, -2) in order to make the area of his garden 20 square feet.

Using the given vertices and the formula for the area of a rectangle,

Area = Length * Width

Given vertices:

A(-1, 2)

B(-1, -2)

The length of the rectangle is the difference in the x-coordinates of the two given vertices, and the width is the difference in the y-coordinates.

Length =
`|x_A - x_B| = |-1 - (-1)| = 0 \text{ feet}`

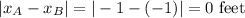
Width =
`|y_A - y_B| = |2 - (-2)| = 4 \text{ feet}`

To find the missing length. Let's call the missing vertices C and D:

Area} = 20 = Length * Width

20 = Length * 4

Length =
`(20)/(4) = 5 \text{ feet}`

To find the missing coordinates, we add 5 to the x-coordinate of the given vertices:

C = (-1 + 5, 2) = (4, 2)

D = (-1 + 5, -2) = (4, -2)

Therefore, Max should have the other two vertices at (4, 2) and (4, -2) in order to make the area of his garden 20 square feet.

Complete question:

Max is drawing plans for a garden, measured in feet, which is shown below on the coordinate plane. Max has two vertices

of the garden at points (-1, 2) and (-1,-2).

At which points should Max have the other two vertices in order to make the area of his garden 20 square feet?