Question

PLEASE HELP
Blank # 1
Blank # 2
Blank # 3
Blank # 4

Answer 1

The endpoints coordinates are calculated, using the midpoint formula, as: (-2, -1) and (1, 0).

What is the midsegment of a triangle?

The midsegment of a triangle is a line segment connecting the midpoints of two sides, parallel to the third side and equal to half its length, thus, we would apply the midpoint formula to find the endpoint coordinates.

The midpoint formula is given by:

`\[ M = \left( \frac{{x_1 + x_2}}{2}, \frac{{y_1 + y_2}}{2} \right) \]`

Find the midpoint between points B(-3, 1) and D(-1, -3):

`M_x = \frac{{-3 + (-1)}}{2}`

`M_y = \frac{{1 + (-3)}}{2}`

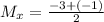
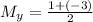
Solving these equations:

`M_x = \frac{{-4}}{2} = -2`

`M_y = \frac{{-2}}{2} = -1`

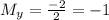
So, the midpoint between points B and D is (-2, -1).

Find the midpoint between points C(3, 3) and D(-1, -3):

`M_x = \frac{{3 + (-1)}}{2}`

`M_y = \frac{{3 + (-3)}}{2}`

`M_x = \frac{{2}}{2} = 1`

`M_y = \frac{{0}}{2} = 0`

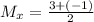
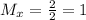
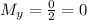
(1, 0).

Thus, the endpoints coordinates would be: (-2, -1) and (1, 0).

Complete Question:

What are the endpoint coordinates of the midsegment of triangle BCD that is parallel to side BC?