Question

Help me with those two questions

Answer 1

Given:

A figure in which a transversal line intersect two parallel lines.

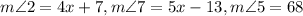`m\angle 2=4x+7, m\angle 7=5x-13, m\angle 5=68` and
`m\angle 3=3y-2`.

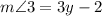To find:

The value of x and y.

Solution:

We know that, if a transversal line intersect two parallel lines, then

(1) Alternate exterior angles are equal.

(2) Same sided interior angles are supplementary. So their sum is 180 degrees.

In the given figure j and k are parallel lines and l is a transversal line.

From the given figure, it is clear that,

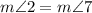`m\angle 2=m\angle 7` (Alternate exterior angles are equal)

`4x+7=5x-13`

`7+13=5x-4x`

`20=x`

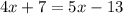
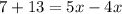
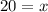
Therefore, the value of x is 20.

Now,

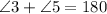`\angle 3+\angle 5=180` (Same sided interior angles are supplementary)

`3y-2+68=180`

`3y+66=180`

`3y=180-66`

`y=(180-66)/(3)`

`y=(114)/(3)`

`y=38`

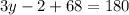
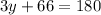
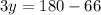
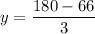
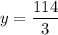
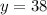
Therefore, the value of y is 38.