Question

If P is the circumvented of triangle ABC, AD= 3x-11, DV= 5x -29, and PC= 18, FIND DP

Answer 1

Since P is the circumcenter △ABC, the length of segment DP is equal to 8.3 units.

In Mathematics and Euclidean Geometry, a circumcenter is the point where perpendicular bisectors (right-angled lines to the midpoint) of the sides of a triangle meet together or intersect.

Since, DP bisects AB, it implies that segment AB must be equal to segment DB;

AB = DB

3x - 11 = 5x - 29

5x - 3x = 29 - 11

2x = 18

x = 18/2

x = 9

For the length of segment DB, we have:

DB = 5x - 29

DB = 5(9) - 29

DB = 16

Next, we would determine the length of segment DP by applying Pythagorean theorem to triangle DPB as follows;

`PB^2 = DB^2 + DP^2\\\\DP^2 = PB^2 - DB^2\\\\DP^2 = 18^2 - 16^2\\\\DP^2 = 324 - 256\\\\DP^2 = 68\\\\DP = √(68)`

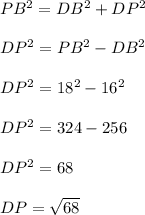
DP = 8.2462 ≈ 8.3 units.

Complete Question:

If P is the circumcenter △ABC, and AD =3x - 11, DB = 5x - 29, PC = 18, find DP.