Question

Anthony claims that is an isosceles triangle. Q4 Find the length of using the distance formula. LM = _________

Answer 1

In △LMN, Anthony claims it is isosceles. Calculating the length of segment LM using the distance formula yields
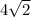`\(4√(2)\)`, confirming Anthony's claim and providing a quantitative measure of the triangle's side.

The distance (d) between two points
`\((x_1, y_1)\)` and
`\((x_2, y_2)\)` is calculated using the distance formula:

`\[ d = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]`

For segment LM
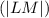`(\(|LM|\))`, using coordinates (L (3, 4)) and (M (7, 8)):

`\[ |LM| = √((7 - 3)^2 + (8 - 4)^2) \]`

`\[ |LM| = √(4^2 + 4^2) \]`

`\[ |LM| = √(32) \]`

Thus, the length of segment LM is
`\(|LM| = 4√(2)\)`.

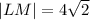The question probable may be:

Anthony asserts that △LMN is an isosceles triangle. Given the coordinates of points (L (3, 4)), (M (7, 8)), and (N (5, 12)), calculate the length of segment LM using the distance formula.