Question

A guy throws a ball at 30 degrees above the horizontal at a velocity of 27 m/s

(what are the formulas for vertical/horizontal initial velocity?)

What is the the initial vertical and horizontal velocities

What is the time to reach the maximum height and the total time

What is the maximum height

What is the total distance traveled

Answer 1

`Initial vertical velocity: \(v_(0y) = 13.5 \, \text{m/s}\), horizontal velocity: \(v_(0x) = 23.4 \, \text{m/s}\). Time to max height: \(t_{\text{max}} = 1.38 \, \text{s}\). Max height: \(H = 9.15 \, \text{m}\). Total distance: \(D = 32.6 \, \text{m}\).`

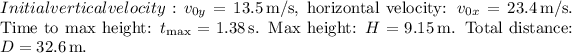
To solve this problem, we can use the following kinematic equations for projectile motion. Let's denote:

-
`\( v_0 \)` as the initial velocity (27 m/s),

-
`\( \theta \)` as the launch angle (30 degrees),

-
`\( g \)` as the acceleration due to gravity (approximately 9.8 m/s²).

The horizontal (x) and vertical (y) components of the initial velocity
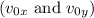`(\(v_(0x)\) and \(v_(0y)\))` can be found using trigonometric functions:

`\[ v_(0x) = v_0 \cdot \cos(\theta) \]`

`\[ v_(0y) = v_0 \cdot \sin(\theta) \]`

1. Initial vertical and horizontal velocities:

`\[ v_(0x) = 27 \cdot \cos(30^\circ) \]`

`\[ v_(0y) = 27 \cdot \sin(30^\circ) \]`

2. Time to reach the maximum height
`(\(t_{\text{max}}\)):`

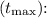
The time to reach the maximum height is given by the formula:

`\[ t_{\text{max}} = (v_(0y))/(g) \]`

3. Total time of flight
`(\(t_{\text{total}}\)):`

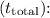
The total time of flight is twice the time to reach the maximum height:

`\[ t_{\text{total}} = 2 \cdot t_{\text{max}} \]`

4. Maximum height
`(\(H\)):`

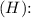
The maximum height can be found using the formula:

`\[ H = (v_(0y)^2)/(2g) \]`

5. Total distance traveled
`(\(D\)):`

The total distance traveled is the horizontal component of the initial velocity multiplied by the total time of flight:

`\[ D = v_(0x) \cdot t_{\text{total}} \]`