Answer:
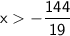
Explanation:
Let's solve the given inequality:
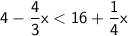
First, let's simplify the inequality:
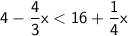
Multiply both sides by 12 to clear the denominators:
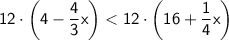
Simplify:
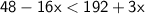
Now, let's isolate
 :
:
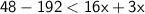
Combine like terms:
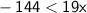
Divide by 19 (remembering to reverse the inequality sign when dividing by a negative number):
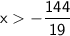
Now, let's graph the solution on a number line. Since
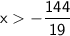 , the solution is all real numbers greater than
, the solution is all real numbers greater than
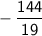 .
.
For a number line: see Attachment
This line represents all real numbers greater than
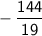 . The open circle at
. The open circle at
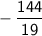 indicates that this value is not included in the solution set.
indicates that this value is not included in the solution set.
Therefore, the solution to the inequality is
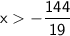 , and it can be represented graphically as shown in attachment.
, and it can be represented graphically as shown in attachment.