Question

According to financial records, 24% of U.S. adults have more debt on their credit cards than they have money in their savings accounts. Suppose that we

take a random sample of 100 U.S. adults. Let D = the number of adults in the
sample with more debt than savings.
a. Explain why D can be modeled by a binomial distribution even though the sample was selected without replacement.
b. Use a binomial distribution to estimate the probability that 30 or more adults in the sample have more debt than savings.

Answer 1

a. D, the number of U.S. adults in a sample with more credit card debt than savings, follows a binomial distribution due to fixed trials, independence, constant probability, and binary outcomes.

b. Using the binomial probability formula, estimate the probability that 30 or more adults in a sample of 100 have more debt than savings.

a. The variable D, representing the number of adults in the sample with more debt than savings, can be modeled by a binomial distribution because it satisfies the following conditions:

1. **Fixed Number of Trials (n):** In this case, the fixed number of trials is the size of the sample, which is 100 U.S. adults.

2. **Independent Trials:** While the sample was selected without replacement, the population is large enough that the probability of selecting an adult with more debt than savings doesn't significantly change from one selection to the next within the sample. Therefore, the trials can be considered independent for practical purposes.

3. **Constant Probability of Success (p):** The probability of success (an adult having more debt than savings) remains constant for each individual in the sample.

4. **Binary Outcome:** Each individual in the sample can be classified as either having more debt than savings (success) or not having more debt than savings (failure).

Given these conditions, D follows a binomial distribution.

b. To estimate the probability that 30 or more adults in the sample have more debt than savings, you can use the binomial probability formula:

`\[ P(X \geq k) = \sum_(i=k)^(n) \binom{n}{i} p^i (1-p)^(n-i) \]`

where:

- \( n \) is the number of trials (sample size),

- \( k \) is the number of successes (adults with more debt than savings),

- \( p \) is the probability of success (the proportion of U.S. adults with more debt than savings according to financial records), and

-
`\( \binom{n}{i} \)` is the binomial coefficient, representing the number of ways to choose \( i \) successes out of \( n \) trials.

In this case,
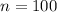`\( n = 100 \)` (sample size) and
`\( p = 0.24 \)`(proportion of U.S. adults with more debt than savings). You want to find
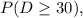`\( P(D \geq 30) \),` so \( k = 30 \).

`\[ P(D \geq 30) = \sum_(i=30)^(100) \binom{100}{i} (0.24)^i (0.76)^(100-i) \]`