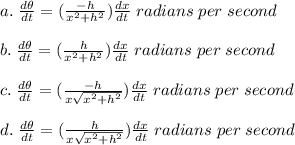An equation that best describes the relationship between dθ/dt, the rate of change of θ with respect to time, and dh/dt, the rate of change of h with respect to time is: A.
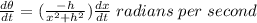
In Mathematics, the tangent trigonometric ratio can be modeled by the following formula;
Tan(θ) = Opp/Adj
Where:
- Adj represents the adjacent side of a right-angled triangle.
- Opp represents the opposite side of a right-angled triangle.
- θ represents the angle.
Based on the information provided about the right triangle with base x meters and height h meters, we have the following tangent trigonometric ratio:
tanθ = h/x
Note:
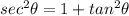 and
and
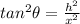
By taking the first derivative of θ with respect to t, we have:
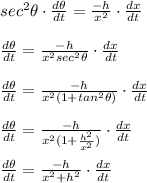
Complete Question:
A right triangle has base x meters and height h meters, where h is constant and x changes with respect to time t, measured in seconds. The angle θ, measured in radians, is defined by tanθ=h/x.
Which of the following best describes the relationship between dθ/dt, the rate of change of θ with respect to time, and dx/dt, the rate of change of h with respect to time?