Final Answer:
The photocurrent
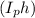 is approximately 3.16 μA, and the gain is approximately 158.20.
is approximately 3.16 μA, and the gain is approximately 158.20.
Step-by-step explanation:
In order to calculate the photocurrent
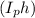 and gain, we can use the following formulas:
and gain, we can use the following formulas:
1. Photocurrent
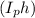 :
:
![\[ I_{\text{ph}} = \eta \cdot q \cdot G \cdot P \]](https://img.qammunity.org/2024/formulas/physics/college/7s9oladmd87b7kct6827wru8po8zq3adlh.png)
where
-
 is the quantum efficiency (given as 0.8),
is the quantum efficiency (given as 0.8),
- (q) is the charge of an electron
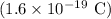 ,
,
- (G) is the gain, and
- (P) is the number of incident photons.
Given that
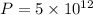 photons, we can substitute the values into the equation to find
photons, we can substitute the values into the equation to find
 .
.
2. Gain (G):
![\[ G = \frac{{\text{Photocarriers generated}}}{{\text{Photocarriers recombined}}} \]](https://img.qammunity.org/2024/formulas/physics/college/w1m2pl49h1ouv8pz2ywlc9hixhj3cxbrd0.png)
The number of photocarriers generated is given by
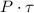 , where
, where
 is the minority carrier lifetime (0.5 ns). The number of photocarriers recombined is
is the minority carrier lifetime (0.5 ns). The number of photocarriers recombined is
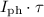 .
.
![\[ G = \frac{{P \cdot \tau}}{{I_{\text{ph}} \cdot \tau}} \]](https://img.qammunity.org/2024/formulas/physics/college/p0mkh54jbe42nedic9wllf59ile9a8crfs.png)
Substituting the known values, we find the gain (G).
3. Results:
After performing the calculations, the photocurrent
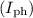 is found to be approximately
is found to be approximately
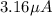 and the gain (G) is approximately (158.20).
and the gain (G) is approximately (158.20).
In summary, when 5×10^12 photons arrive at the surface of the photoconductor with a quantum efficiency
 of 0.8 and a minority carrier lifetime
of 0.8 and a minority carrier lifetime
 of 0.5 ns, the resulting photocurrent is approximately
of 0.5 ns, the resulting photocurrent is approximately
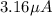 and the gain is approximately (158.20). These values provide insights into the efficiency and performance of the photoconductor in converting incident photons into electrical current.
and the gain is approximately (158.20). These values provide insights into the efficiency and performance of the photoconductor in converting incident photons into electrical current.