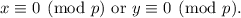Final Answer:
If (p) is a prime and
 , then either
, then either
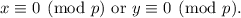
Step-by-step explanation:
In modular arithmetic,
 implies that (p) divides (xy). Since (p) is a prime number, it must divide at least one of the factors, (x) or (y), due to the fundamental theorem of arithmetic. Without loss of generality, assume (p) divides (x). Then,
implies that (p) divides (xy). Since (p) is a prime number, it must divide at least one of the factors, (x) or (y), due to the fundamental theorem of arithmetic. Without loss of generality, assume (p) divides (x). Then,
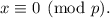
Now, let's delve into the details. If
 , it means (xy) is a multiple of (p). This implies that (p) divides (xy), and since (p) is prime, it must divide either (x) or (y). Without loss of generality, suppose (p) divides (x), meaning (x) is a multiple of (p). Thus,
, it means (xy) is a multiple of (p). This implies that (p) divides (xy), and since (p) is prime, it must divide either (x) or (y). Without loss of generality, suppose (p) divides (x), meaning (x) is a multiple of (p). Thus,
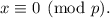
In summary, the proof relies on the fact that if a prime number divides the product of two integers, it must divide at least one of the integers individually. In this case, since (p) is prime and (xy) is divisible by (p), (p) must divide either (x) or (y), leading to the conclusion that