Final Answer:
1. For
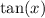 , the fifth-degree Taylor series expansion about ( a = 0 ) is
, the fifth-degree Taylor series expansion about ( a = 0 ) is
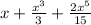 .
.
2. For
 , the fifth-degree Taylor series expansion about ( a = 0 ) is
, the fifth-degree Taylor series expansion about ( a = 0 ) is
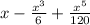 .
.
3. These approximations can be used to estimate values of
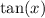 and
and
 near ( x = 0 ) by substituting the corresponding series expressions.
near ( x = 0 ) by substituting the corresponding series expressions.
Explanation:
The Taylor series expansions for
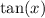 and
and
 centered at ( a = 0 ) up to the fifth degree provide polynomial approximations that capture the behavior of these functions in the vicinity of zero.
centered at ( a = 0 ) up to the fifth degree provide polynomial approximations that capture the behavior of these functions in the vicinity of zero.
For
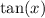 , the expansion
, the expansion
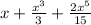 is derived from the derivatives of
is derived from the derivatives of
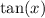 evaluated at ( a = 0 ). The series is designed to closely mimic the behavior of
evaluated at ( a = 0 ). The series is designed to closely mimic the behavior of
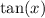 for small values of ( x ).
for small values of ( x ).
Similarly, for
 , the expansion
, the expansion
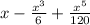 is obtained by evaluating the derivatives of
is obtained by evaluating the derivatives of
 at ( a = 0 ). This polynomial approximation is particularly accurate for ( x ) near zero, capturing the sine function's oscillatory behavior.
at ( a = 0 ). This polynomial approximation is particularly accurate for ( x ) near zero, capturing the sine function's oscillatory behavior.
These Taylor series are powerful tools in calculus and mathematical analysis, enabling the estimation of function values and behavior in regions around a chosen center. As the degree of the series increases, the accuracy of the approximation improves, making them valuable for various mathematical and scientific applications.