Question

naval intelligence reports that 9 enemy vessels in a fleet of 23 are carrying nuclear weapons. if 10 vessels are randomly targeted and destroyed, what is the probability that more than 1 vessel transporting nuclear weapons was destroyed? express your answer as a fraction or a decimal number rounded to four decimal places.

Answer 1

The probability that more than 1 vessel transporting nuclear weapons was destroyed is approximately 0.2848, rounded to four decimal places.

To solve this problem, we can use the complement probability.

The probability of more than 1 vessel carrying nuclear weapons being destroyed is equal to 1 minus the probability of 0 or 1 vessel carrying nuclear weapons being destroyed.

Let's calculate the probability of 0 or 1 vessel carrying nuclear weapons being destroyed:

The probability of a vessel carrying nuclear weapons being destroyed in a single attempt is the ratio of the number of vessels carrying nuclear weapons to the total number of vessels.

In this case, it is 9/23.

Therefore, the probability of a vessel carrying nuclear weapons not being destroyed in a single attempt is 1 - 9/23 = 14/23.

Now, we can calculate the probability of 0 or 1 vessel carrying nuclear weapons being destroyed in 10 attempts.

We can use the binomial probability formula:

P(X≤1)= (
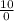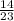`(10)/(0)` ) (
`(14)/(23)` )^10 + (
`(10)/(1)` ) (
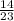`(14)/(23)` )^9 (
`(9)/(23)` )

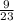Using a calculator or statistical software, we find this probability to be approximately 0.7152.

Finally, the probability of more than 1 vessel carrying nuclear weapons being destroyed is:

P(More than 1)=1−P(X≤1)

P(More than 1)≈1−0.7152≈0.2848

So, the probability that more than 1 vessel transporting nuclear weapons was destroyed is approximately 0.2848, rounded to four decimal places.